Introduction
The emergence of blockchain technology has helped solve issues related to privacy and anonymity in a heavily centralized world. Functioning as an unchangeable digital ledger, blockchain utilizes various cryptographic methods to achieve the utmost security when exchanging information. Among these methods is the use of zero-knowledge proofs or ZKPs. Working with carefully crafted algorithms, this technique provides users with the ability to verify their data without revealing what that data is.
In a world where personal data has become more or less a commodity, this kind of advantage is monumental. It could potentially mean the elimination of common security risks, such as the stealing of financial information or identity fraud. By taking a step further and combining zero-knowledge proofs with blockchain technology, a powerful mix of immutability and security can be achieved.
Before we discuss the various use cases for ZKPs as well as their role in the blockchain world further, let us first attempt to understand the basics of how this cryptographic method works.
Zero-Knowledge Proofs Explained
Despite being regarded as a major component of the blockchain space today, ZKPs precede the inception of blockchain technology by over 40 years. In 1985, MIT researchers Silvio Micali, Shafi Goldwasser, and Charles Rackoff proposed the concept of zero-knowledge proofs as a new innovation in applied cryptography.
In their research paper, they discussed an interesting new metric which they termed knowledge complexity. This measured the amount of knowledge that is needed to transfer from a prover to a verifier for the information being exchanged between them to be considered valid. Building on this idea, they were able to prove that with some interaction between a prover and a verifier, the amount of knowledge that needed to be conveyed could be reduced from two to zero. The method used to achieve this was hence coined as zero-knowledge proof- the applications for which are being seen in various forms today.
Properties of Zero-knowledge Proofs
There are three major properties every zero-knowledge proof must include as part of its definition.
Completeness
The first property is completeness. This refers to the idea that if a statement made by the prover during an exchange is true, then the verifier on the other end can be convinced of this fact eventually and without any external help.
Soundness
The second property is soundness. This can be understood as the mirror image of completeness, dealing with a statement that is not true. The soundness property dictates that if the information the prover is providing is false, there is no way to convince the verifier that it is true.
Zero-knowledge
The third and most critical property in defining a ZKP is the property of zero-knowledge. This refers to the notion that regardless of whether the information presented is true or false, the verifier must not learn anything about the information being exchanged.
Types of Zero-knowledge Proofs
There are two broad categories of ZKPs, namely interactive and non-interactive. Let us try to understand each type individually with the help of an example.
Interactive
Interactive proofs require several interactions between the prover and verifier. The verifier continues to challenge the prover regarding the validity of the statement put forward until he is finally convinced. We can use an example to explain this with more clarity.
Let us say there exists a cave which on entering leads to two passages. Both passages lead to a dead end, though there is a way to get from one passage to the other through the use of a magic door. This magic door can only be accessed by a secret password. If a user knows this secret password, he can access the door and hence come out of the page through the other passage. Otherwise, he will be stuck inside.
Here is a depiction of this cave in question. Between passages C and D exists a magic door that can be opened with a secret password.
Suppose Alice and Bob both visit this cave at the same time. Alice claims to know the secret password required to move between these two passages, and can prove it to Bob without revealing it. In this scenario, Alice is the prover while Bob is the verifier of the secret.
First, Alice enters the cave from any passage she wants. Bob, unaware of which passage she entered from, calls out the passage he wants her to appear from. If Alice had entered from passage C and Bob called out passage D, she would have needed to use the secret password to open the magic door and hence fulfill his request. However, if Alice had entered passage C and Bob had also called out passage C, she could have just turned around and retraced her steps to appear from the opening she entered from. Alice would not need to access the magic door but could fool Bob into believing she knew the password as technically she did fulfill his request of appearing from passage C.
To reduce the chances of this happening, the interaction is repeated many times between Bob and Alice. If Alice is successful in each attempt, the chances of her successfully anticipating all of Bob’s requests becomes increasingly small. Hence, it is proven that Alice knows this secret without revealing any information about what that secret is.
Non-interactive
Non-interactive zero-knowledge proofs work to achieve the same outcome of verifying with zero knowledge but without any interaction between the prover and verifier. An implementation of this is zk-SNARKS, a type of cryptographic proof that popular solutions like Tornado Cash and zCash are based on. We can use the procedure followed by the privacy solution Tornado Cash as an example to better understand this.
Initially, a user is provided with a randomly generated key known as a note. The hash of this note is then supplied to the Tornado Cash smart contract along with the amount of Ether a user wishes to send. You can think of this as the smart contract containing a pool of a large sum along with many hashes of notes.
When a user decides to withdraw their amount, they can simply submit the hash they had initially shown to the Tornado Cash smart contract. The existence of this hash will prove that their money was deposited, without revealing what that hash was. In this way, the proof is verified without any interaction between the prover and verifier.
Zero-Knowledge Proofs in the Blockchain World
The applications zero-knowledge proofs can offer the blockchain world are endless. Use cases of this technology currently being discussed include security of data from third parties, added controls over file system access, and identity verification of a user without revealing any personal information.
EY has also announced the release of a new tool using ZKP technology known as Nightfall. This tool would allow transactions made on Ethereum to become private, allowing companies operating on the public blockchain to preserve confidentiality in their business dealings. As the hunt for privacy remains a long-withstanding priority for users on the pseudonymous blockchain, the benefits of a service like this are much-needed.
Moving Forward
Understanding the importance of zero-knowledge proofs may be imperative for developing innovations in the blockchain space. Moreover, combining ZKPs with blockchain technology can result in major advancements, providing much-needed security and scalability to our platforms. It is highly sermonized that blockchain development companies come up with solutions that complement zero-knowledge proofs.
References
https://z.cash/technology/zksnarks/
https://medium.com/coinmonks/zero-knowledge-proofs-14bb012c1ce9
 BlockApex
BlockApex  November 23, 2021
November 23, 2021 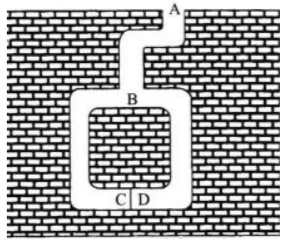

 BlockApex
BlockApex  April 6, 2022
April 6, 2022